Calcul simplifié des pertes de charges selon DTU 60.11 - Paragraphe 5.5 (Formule de Colebrook)
Introduction aux pertes de charges
Les pertes de charges dans une installation de plomberie sont dues à la friction du fluide sur les parois des tuyaux. Le DTU 60.11 propose une méthode dite simplifié pour l'évaluation de la perte de charge selon la formule de Colebrook.
Notre formulaire propose le calcul exact des pertes de charges et non l'application de la formule simplifiée
Abaque de pertes de charge simplifié DTU 60.11 - Résolution Graphique
Utilisez votre souris ou votre doigt pour interagir avec le graphique. Tracer deux points pour créer la droite correspondant aux conditions initiales, l'intersection avec les échelles correspondent aux résultats recherchés.
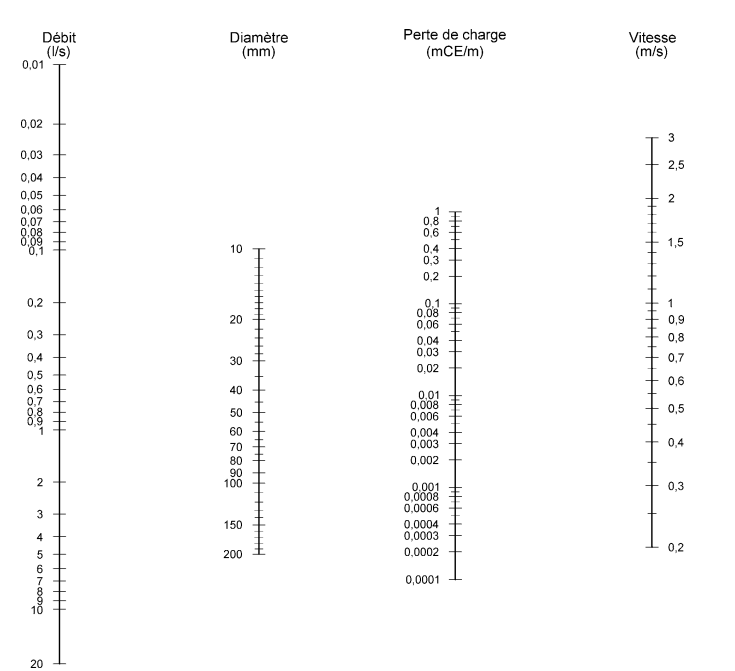
Résolution numérique - Exacte et simplifiée
Rugosité
Conditions
Méthode 1 : A partir du débit (m3/h)
Méthode 2 : A partir de la vitesse du fluide (m/s)
Calculpro.fr est un site internet gratuit, sans publicité, sans sponsoring. En créant un compte, vous nous aider à faire grandir la communauté et de l'engagement!
Explication de la méthode de calcul simplifié
Comprendre et Calculer les Pertes de Charge : La Méthode Simplifiée du DTU 60.11
En plomberie, la conception d'un réseau de distribution d'eau efficace passe par une maîtrise des pertes de charge. Celles-ci représentent la diminution de la pression de l'eau due aux frottements dans les canalisations. Le DTU 60.11, document technique de référence pour les installations de plomberie sanitaire, propose des méthodes de calcul précises. Parmi elles, une approche simplifiée permet d'estimer rapidement ces pertes de charge, un atout majeur pour les professionnels sur le terrain.
La base théorique : De Colebrook à la simplification
Le calcul théorique des pertes de charge, notées ΔP, se base sur des formules complexes comme celle de Darcy-Weisbach, qui fait intervenir un coefficient de perte de charge Λ (Lambda). Ce coefficient est lui-même déterminé par la formule de Colebrook :
1/√Λ = -2 log( (ε / 3,7D) + (2,51 / (Re√Λ)) )
Cette équation prend en compte la rugosité des parois (ε), le diamètre de la canalisation (D) et le nombre de Reynolds (Re), qui caractérise le régime d'écoulement du fluide. Bien que très précise, sa complexité la rend difficile à utiliser pour des calculs rapides.
L'hypothèse clé pour la simplification selon le DTU 60.11
Pour faciliter le travail des concepteurs et installateurs, le DTU 60.11 propose une simplification basée sur une hypothèse réaliste. On considère une rugosité (ε) constante de 0,0001 m. Cette valeur n'est pas celle du matériau neuf, mais une valeur moyenne qui anticipe la formation de dépôts et l'entartrage de la canalisation après plusieurs mois d'utilisation. C'est une approche pragmatique qui garantit la performance du réseau sur le long terme.
La formule de calcul simplifiée des pertes de charge
Grâce à cette hypothèse, on aboutit à une formule directe pour calculer la perte de charge linéaire (J), c'est-à-dire la perte de pression par mètre de tuyau.
La première formule exprimée en Pascals par mètre (Pa/m) est la suivante :
J = 5,65 x V1,896 / D1,276
- J : Perte de charge linéaire en Pascals par mètre (Pa/m).
- V : Vitesse de l'eau en mètres par seconde (m/s).
- D : Diamètre intérieur de la canalisation en mètres (m).
Une formule encore plus pratique pour les chantiers
Pour une utilisation encore plus intuitive, le DTU 60.11 décline cette équation avec des unités plus courantes en plomberie. La perte de charge est exprimée en mètre de colonne d'eau par mètre (mCE/m) et le diamètre en millimètres (mm), ce qui correspond aux standards des fournisseurs.
Cette version, la plus utilisée, s'écrit :
J = 3,8 x V1,896 / D1,276
- J : Perte de charge linéaire en mètres de colonne d'eau par mètre (mCE/m).
- V : Vitesse de l'eau en mètres par seconde (m/s).
- D : Diamètre intérieur de la canalisation en millimètres (mm).
Cette formule simplifiée est un outil puissant pour le dimensionnement des réseaux d'eau froide et d'eau chaude sanitaire. Elle offre un excellent compromis entre précision et facilité de mise en œuvre, en parfaite conformité avec les exigences du DTU 60.11. Pour des déterminations encore plus rapides, l'abaque (diagramme graphique) tiré de cette formule reste une alternative très efficace.